1. 트리의 운행법
Root가 앞(Pre)에 있으면 Preorder
Root가 안(In)에 있으면 Inorder
Root가 뒤(Post)에 있으면 Postorder

- Preorder 운행 : Root -> Left -> Right ( A, B, C )
- Inorder 운행 : Left -> Root -> Right ( B, A, C )
- Postorder 운행 : Left -> Right -> Root ( B, C, A )
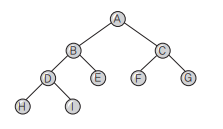
- Preorder 운행 : A B D H I E C F G
- Inorder 운행 : H D I B E A F C G
- Postorder 운행 : H I D E B F G C A
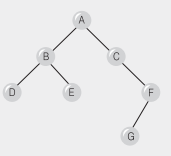
- Inorder 운행 : D B E A C G F
2. 수식의 표기법
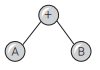
- 전위 표기법(PreFix) : 연산자 -> Left -> Right ( +AB )
- 중위 표기법(InFix) : Left -> 연산자 -> Right ( A+B )
- 후위 표기법(PostFix) : Left -> Right -> 연산자 ( AB+ )
Infix - 연산자가 안에
Prefix - 연산자가 앞에
Postfix - 연산자가 뒤에
1. 중위식(Infix)을 후위식(Postfix)로 변환하기
[보기 1] X = A / B * (C + D) + E
* 연산 우선순위에 따라 괄호로 묶기
( X = ( ( (A / B) * (C + D) ) + E ) )
* 연산자를 해당 괄호의 뒤(오른쪽)으로 옮기기
( X ( ( (A B) / (C D) + ) * E ) + ) =
* 필요 없는 괄호 제거
X A B / C D + * E + =
[보기 2] X = A + ( B + C / D ) x E - F
X A B C D / + E x + F - =
2. 중위식(Infix)을 전위식(Prefix)로 변환하기
[보기 1] X = A / B * (C + D) + E
* 연산 우선순위에 따라 괄호로 묶기
( X = ( ( (A / B) * (C + D) ) + E ) )
* 연산자를 해당 괄호의 앞(왼쪽)으로 옮기기
= ( X + ( *( / (AB) + (CD) ) E) )
* 필요 없는 괄호 제거
= X + * / A B + C D E
3. 후위식(Postfix)를 중위식(Infix)으로 변환하기
[보기 1] A B C - / D E F + * +
* 인접한 피연산자 두 개와 오른쪽의 연산자를 괄호로 묶기
( (A (B C -) /) (D(E F +) *) + )
* 연산자를 해당 피연산자의 가운데로 이동
( ( A / ( B - C ) ) + ( D * ( E + F ) ) )
* 필요 없는 괄호 제거
A / (B - C) + D * (E + F)
[보기 2] ABC - / DEF + * +
A / (B - C) + D * (E + F)
4. 전위식(Prefix)를 중위식(Infix)으로 변환하기
[보기 1] + / A - B C * D + E F
* 인접한 피연산자 두 개와 왼쪽의 연산자를 괄호로 묶기
( + (/ A (- B C)) (* D (+ E F)) )
* 연산자를 해당 피연산자 사이로 이동
(( A /(B-C)) + ( D*(E+F)))
* 필요 없는 괄호 제거
A / (B - C) + D * (E + F)
[보기 2] - + * A B C / D E
A * B + C - D / E
* 2020년 1, 2회 통합 정보처리기사 필기 기출문제
예) 다음 트리의 전위 순회(Preorder Traversal)한 결과는?
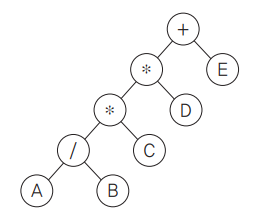
Preorder : Root -> Left -> Right
-> +**/ABCDE
* 이 게시물은 시나공 교재를 참고로 작성되었습니다.
'정보처리기사 > 정보처리기사 필기' 카테고리의 다른 글
| 정보처리기사 필기 ) 선점 스케줄링 (0) | 2020.08.12 |
|---|---|
| 정보처리기사 필기 ) 비선점 스케줄링 (0) | 2020.08.12 |
| 정보처리기사 2020 1, 2회 통합 기출문제 풀이 - 3과목 ( 오답 ) (0) | 2020.08.12 |
| 정보처리기사 2020 1, 2회 통합 기출문제 풀이 - 2과목 ( 오답 ) (0) | 2020.08.12 |
| 정보처리기사 2020 1, 2회 통합 기출문제 풀이 - 1과목 ( 오답 ) (0) | 2020.08.12 |




댓글